Growing Neural Cellular Automata

Quentin Wach

The next level in AI is self-organization. That is one of the reasons for why I am deeply interested in cellular automata. So I’ve been implementing various papers recently. Here is a blog post about GNCAs.

Introduction

Growing Neural Cellular Automata (GNCA)¹ are inspired by how multicellular organisms develop from a single cell into complex forms. Rather than being given a simple set of rules like normal cellular automata, GNCA learn the rules within their internal neural network i.e. they are differentiable cellular automata that learn self-organizing patterns. Amzingly, we can train them to grow from a single cell and regenerate when damaged. If you think about how they do that, you’ll realize that means the automata will not just need to learn a simple update rule but actually how to communicate with their neighbouring cells to collaboratively organize into the given morphology. Morphogenesis!

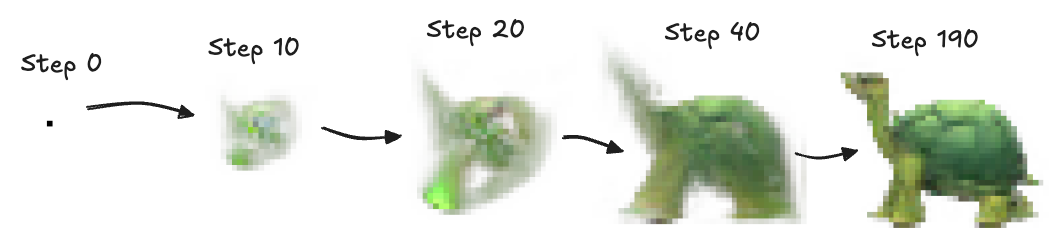
Below, I will explain GNCA, implement it step by step, and demonstrate these abilities.

Neural Cellular Automata

Imagine a white image. To illustrate the power of neural cellular automata (NCA), we will create one which learns to form images like that of a turtle shown above. That means, every pixel in the image is a single NCA which interacts with its own state as we step through time and with the state of all the eight neighbouring NCAs. It is often immediately assume that the interactions here are not in fact purely local because of how complex the shapes are that NCAs can assemble into but this is in fact true! How?

Perception

The key is to augment the state and perception of the NCAs neighboring states with additional channels and filters.

Channels

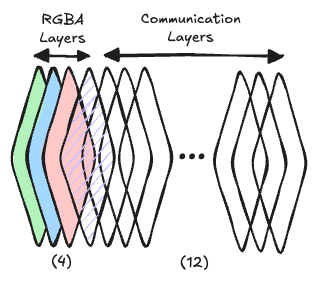
While the perception and computation of every NCA is purely local, it is not just based on the visible pixels. Most of the computation and communication with neighbouring NCAs happens in invisble layers meant for that exact purpose. So rather than just having an red, green, blue, and alpha channel, each cell maintains a 16-dimensional state vector where

channels 0-2 encode the RGB color values,
channel 3 is the alpha channel (\(\alpha\)) and acting like a “life” indicator, and
channels 4-15 are hidden channels for internal computation & communication.

The alpha channel is crucial as well. Cells with \(\alpha > 0.1\) are considered “alive” and can influence neighbors. Cells without living neighbors are explicitly zeroed out.

Filters

We further augment the perception of the NCAs by adding three fixed Sobel filters to each layer, two in order to detect the local gradients and one to detect its own cell state. This creates a 48-dimensional perception vector (16 channels × 3 operations) for each cell.

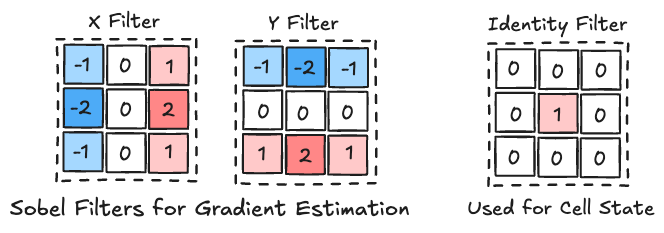
The filters act as a preprocessing step that highlights important features, enabling the NCA to focus on relevant information and ignore noise. This helps to stabilize the learning process. Without the Sobel filters, the NCA tend to struggle to discern subtle differences in cell states, leading to erratic or suboptimal behavior.

Implementation

Below, you can find my implementation of this perception pre-processing step for each channel. Note that I have also included rotations of the filters given an angle. In the original paper, you can set an angle which will rotate the structures since the update rules have been rotated with it. This is fun but I don’t find it particularly interesting so I will not further mention it here.

class Perception(nn.Module):

    def __init__(self, channel_n, angle=0.0):
        super().__init__()
        
        # Sobel filters for gradient estimation
        sobel_x = torch.tensor([
            [[-1, 0, 1],
             [-2, 0, 2], 
             [-1, 0, 1]]
        ], dtype=torch.float32)
        
        sobel_y = torch.tensor([
            [[-1, -2, -1],
             [ 0,  0,  0],
             [ 1,  2,  1]]
        ], dtype=torch.float32)
        
        # Rotate Sobel filters if angle is provided
        if angle != 0.0: sobel_x, sobel_y = self._rotate_sobel(sobel_x, sobel_y, angle)
        
        # Identity filter (cell's own state)
        identity = torch.tensor([
            [[0, 0, 0],
             [0, 1, 0],
             [0, 0, 0]]
        ], dtype=torch.float32)
        
        # Combine all filters
        kernels = torch.cat([identity, sobel_x, sobel_y], dim=0)
        kernels = kernels[:, None, :, :]  # Add input channel dimension
        
        self.register_buffer('kernels', kernels)
        self.channel_n = channel_n
    
    def _rotate_sobel(self, sobel_x, sobel_y, angle):
        cos_a = torch.cos(torch.tensor(angle))
        sin_a = torch.sin(torch.tensor(angle))
                
        # Apply rotation: [Kx', Ky'] = R * [Kx, Ky]
        rotated_x = cos_a * sobel_x - sin_a * sobel_y
        rotated_y = sin_a * sobel_x + cos_a * sobel_y
        
        return rotated_x, rotated_y
    
    def forward(self, x):
        # Apply perception filters to all channels
        perception_layers = []
        
        for i in range(3):  # identity, sobel_x, sobel_y
            kernel = self.kernels[i:i+1].repeat(self.channel_n, 1, 1, 1)
            conv_result = F.conv2d(x, kernel, padding=1, groups=self.channel_n)
            perception_layers.append(conv_result)
        
        # Concatenate: [identity, grad_x, grad_y] -> 3 * channel_n channels
        return torch.cat(perception_layers, dim=1)

Update

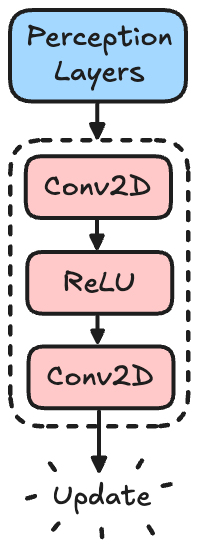
Given the perceived information, the NCA needs to update itself properly. As explained before, rather than writing a hard set of rules, we are instead training a neural network inside the NCA to learn how to update itself.

Update Layers

While the states of the NCAs are quite large due to the many layers, for the neural network, we are simply using 1×1 convolutions to act as per-pixel dense layers. We are using a zero initialization of the final layer to ensure that the cells “do nothing” initially. We also don’t apply a final activation function like ReLU. This allows for both positive and negative update values.

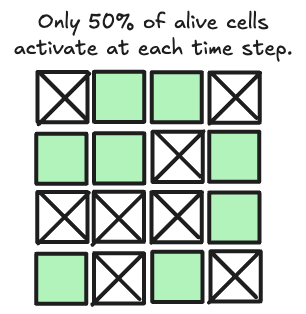
Stochastic Update

To avoid global synchronization, cells update randomly, which we call the “fire rate”. Supposedly, the random timing makes the system more resilient to perturbations.

Living Cells

Using the \(\alpha\)-channel, we also enforce the biological constraint that empty cells remain empty. Another little hack to ensure that we don’t create objects out of thin air due to an accumulation of noisy signals that ramp up to suddenly grow a new object.

Implementation

Including all these considerations, we can write this with PyTorch as:

class NCA(nn.Module):
    def __init__(self, channel_n=16, fire_rate=0.5, angle=0.0):
        super().__init__()
        self.channel_n = channel_n
        self.fire_rate = fire_rate
        self.angle = angle
        
        # Perception layer
        self.perception = Perception(channel_n, angle)
        
        # Update network
        self.update_net = nn.Sequential(
            nn.Conv2d(channel_n * 3, 128, 1),  # 3x perception channels
            nn.ReLU(),
            nn.Conv2d(128, channel_n, 1, bias=False)
        )
        
        # Initialize final layer with small random values instead of zeros
        nn.init.normal_(self.update_net[-1].weight, std=0.01)
    
    def forward(self, x):
        # Perception step
        perception = self.perception(x)
        # Update step
        dx = self.update_net(perception)
        # Stochastic update
        dx = dx * (torch.rand_like(x[:, :1]) <= self.fire_rate).float()
        # Apply update
        x = x + dx
        # Living cell masking
        return self._alive_masking(x)
    
    def _alive_masking(self, x):
        # Cells are alive if alpha > 0.1 in 3x3 neighborhood  
        alpha = x[:, 3:4]  # Alpha channel
        # Use lower threshold for more permissive alive masking
        alive = F.max_pool2d(alpha, 3, stride=1, padding=1) > 0.05
        # Set non-living cells to zero
        return x * alive.float()

The initializatin of the NCA class shows how we are using the perception class as our inputs for the internal sequential 2-layer convolutional network. As described in the forward method, we perceive, calculate the update, coss a toin if we want to apply the update, apply the update, then mask the alive cells.

Learning to Grow & Regenerate

So far we have only defined the Neural Cellular Automata generally. But we could train this architecture in all sorts of ways and on all sorts of data e.g. to reproduce the game of life (even though that would be somewhat absurd). Our goal here though is to show that these NCAs can grow into complex shapes, hold them, and even self-repair if damaged. So aside from the architecture, the key insights of the GNCA paper are in how the NCAs are trained to achieve this!

Initilialization

First, let’s setup yet another new class for this purpose, the Growing Neural Cellular Automata class which takes in the NCA as a model. We’ll add a method load_target to load any image and convert it to RGBA and resize it using the method of nearest neighbors and convert it to a tensor. We also implement a seed method which will create a center pixel from which the GNCA will learn to grow. (You can see this in the first image of this article.) Here is the Python code:

class GNCA:
    def __init__(self, channel_n=16, fire_rate=0.5, device='cpu', angle=0.0):
        self.channel_n = channel_n
        self.fire_rate = fire_rate
        self.device = device
        self.angle = angle
        
        # Create the NCA model
        self.model = NeuralCA(channel_n, fire_rate, angle).to(device)
        
    def load_target(self, path, size=40):
        """Load and preprocess target image"""
        img = Image.open(path).convert('RGBA')
        
        # Use NEAREST for resizing to avoid interpolation artifacts with transparency
        img = img.resize((size, size), Image.NEAREST)
        img = np.array(img).astype(np.float32) / 255.0
        
        # Handle transparency properly - set transparent pixels to zero
        alpha = img[:, :, 3:4]  # Get alpha channel
        img[:, :, :3] = img[:, :, :3] * alpha  # Premultiply RGB by alpha
        
        # Convert to torch tensor [4, H, W]
        img = torch.from_numpy(img).permute(2, 0, 1)
        return img.to(self.device)
    
    def make_seed(self, size, batch_size=1):
        """Create initial seed state"""
        seed = torch.zeros(batch_size, self.channel_n, size, size, device=self.device)
        # Set center pixel: alpha and hidden channels to 1.0
        seed[:, 3:, size//2, size//2] = 1.0
        return seed

Growing

The first experiment presented in the paper is interesting in so far as that it shows that I. we can in fact grow complex shapes from a single seed, and II. the NCAs are not inherently good at holding that shape though. The generated structures are not robust and will quickly diverge and dissolve into abstract shapes.

To show this, we’ll use the ADAM optimizer and the MSE loss to compare the RGBA channels with the target image. As mentioned before, we start with a single pixel seed for every training iteration. During that training iteration, we then let the NCAs update themselves a few dozen times to grow from that seed and generate the shape. We then compare the result with our target and update the weights of the neural network.

Here is the code for the train_basic method we’ll add to the GNCA class for this first experiment:

def train_basic(self, target_path, steps=2000, size=40):
    # Basic training - Experiment 1: Learning to Grow

    target = self.load_target(target_path, size)
    target = target.unsqueeze(0)  # Add batch dimension
    
    # Use lower learning rate and gradient clipping
    optimizer = torch.optim.Adam(self.model.parameters(), lr=1e-3)
    losses = []
    
    for step in tqdm(range(steps)):
        # Use fewer CA steps initially, then increase
        if step < 500: n_steps = np.random.randint(10, 20)  # Start with fewer steps
        else: n_steps = np.random.randint(32, 64)  # Gradually increase
        
        # Start from seed
        x = self.make_seed(size)
        
        # Run CA for n_steps
        for _ in range(n_steps): x = self.model(x)
        
        # Compare RGBA channels with target
        loss = F.mse_loss(x[:, :4], target)
        
        optimizer.zero_grad()
        loss.backward()
        
        # Gradient clipping to prevent exploding gradients
        torch.nn.utils.clip_grad_norm_(self.model.parameters(), max_norm=1.0)
        
        optimizer.step()
        
        losses.append(loss.item())
        
        if step % 100 == 0: print(f"Step {step}, Loss: {loss.item():.6f}")
            
    return losses

Given how basic this first approach is, you’ll immediately realize why the NCAs don’t learn to create patterns that remain stable after being grown. They are just not trained to do so. Still, the authors of the original paper report:

“Growing models were trained to generate patterns, but don’t know how to persist them. Some patterns explode, some decay, but some happen to be almost stable or even regenerate parts!”

How can we improve this?

Pool-Based Persistence

Instead of training on individual trajectories, GNCA uses a state pool to encourage stability.

def train_with_pool():
    # Experiment 2
    # Initialize pool with seed states
    seed = torch.zeros(64, 64, 16)
    seed[32, 32, 3:] = 1.0  # Single living cell in center
    pool = [seed.clone() for _ in range(1024)]
    
    for iteration in range(10000):
        # Sample batch from pool
        batch_indices = random.sample(range(len(pool)), 32)
        batch = [pool[i] for i in batch_indices]
        
        # Always include one seed (prevent catastrophic forgetting)
        batch[0] = seed.clone()
        
        # Run CA for random number of steps
        steps = random.randint(64, 96)
        final_states = model(torch.stack(batch), steps)
        
        # Compute loss against target
        loss = F.mse_loss(final_states[:, :4], target_pattern)
        
        # Update model
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        # Put final states back in pool
        for i, idx in enumerate(batch_indices):
            pool[idx] = final_states[i].detach()

This approach forces the model to learn not just growth, but persistence, the ability to maintain the pattern once formed.

“Persistent models are trained to make the pattern stay for a prolonged period of time. Interstingly, they often develop some regenerative capabilities without being explicitly instructed to do so.”

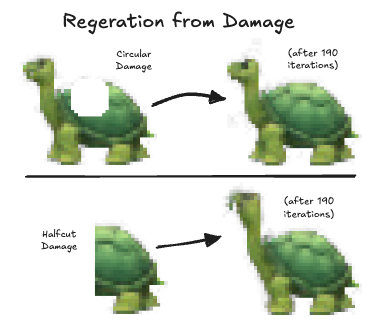
Regeneration

Similarly, by adding a method to damage the structures randomly during training, we can train the GNCA to learn self-repair. I won’t bore you with the details since they are quite derivative from the two previous examples. But here, you can see an example image of how the turtle GNCA repairs itself when damaged in two different ways.

You can find the code for my complete implementation here on GitHub.

Personal Thoughts

There are many more articles I believe would deserve to be discussed in the context of GNCA²³, but here, I will focus on limitations of GNCA, possible future applications and extensions, and some general notes on collaborative / self-organizing AGI.

Issues with Scaling

In order to be able to self-assemble complex structures from only local interactions, the NCA has to learn a long list of update rules to compress all of the information of the target image. As the image becomes more complex, the NCA will require additional layers to capture intricate patterns and dependencies, to hold information in memory and communicate with the neighoring cells.

Since the GNCA assemble based on global interactions only both their performance and robustness could most likely be increased by augmenting these cells with more global perception units⁴ or creating hybrid solutions with purely local and purely global networks.

Going 3D also seems interesting⁵.

Temporal Damage

Currently, the GNCA are extremely good at recovering from damage that is inflicted while the structure is fully grown and stable. That is because this is how they were trained. But if damage is inflicted and varied over multiple steps while the structure attempts to regenerate, the current implementation almost always fails to recover the correct morphology again. It should be easy to extend the training method to account for this issue.

Further Biological Extensions

Since GNCAs were inspired directly by how organisms grow in biology, I want to throw out a few more ideas to extend this further. At the moment, there are three cell states, mature, growing and dead, depending on the value of the alpha channel. Rather than replicating, creating copies, the cells function independently and just pop into existence and differentiate given the neighbor cell states. While we see growth as if the cells were replicating starting from a single cell seed, this growth is implicit. As a result, we do in fact see a lot of cells wandering off alone, popping into existence and vanishing again. There is no explicit rule that only permits cells to grow if they are connected to another mature cell that is ready to replicate. There may be insights into biological morphogenesis to be gained from implementing such biological constraints. I can also imagine that this would signficantly improve the stability and persistence of the GNCA-grown organisms/patterns. Enforcing the rule that cells can only go from dead to alive by copying the state of a neigbor cell as if that cell was replicating would also further constrain the update rules that need to be learned possibly reducing the size and complexity of the GNCA.

Artificial Life & Evolution

Famously, Lenia is also based on the idea of neural cellular automata⁶⁷⁸. As stated in the Lenia article, comparing Lenia and NCA:

“Lenia relies on tuning the parameters of kernels and growth mappings to “train” the model into generating self-organizing patterns, while the incremental update part has limited flexibility. Neural CA, on the other hand, is fixed in the convolutional kernels and activation functions, but heavily parameterized in the fully connected layers. Lenia is aimed at exploring novel patterns, helped by evolutionary, genetic and exploratory algorithms; Neural CA is aimed at generating predefined patterns, results are optimized by gradient descent. Despite the differences, Lenia and Neural CA do one thing in common - exploit the self-organizing, emergenceinducing, and regenerating powers of CAs. Neural CA also exploits the learnable nature of its NN architecture, and it remains unknown whether the Lenia model can be made learnable to achieve other goals.”

I have the vague sense that there may be some interesting ideas hidden at the intersection of GNCA and Lenia.

Design Optimization Problems

In fact, we may consider it a major limitation of this technique (though it was also not the point of the article) that we are predefining the structure that the GNCA form. It will be interesting to explore applications where NCAs are used to actually find optimal structures for any given problem e.g. to design optimal structures for robotics⁹, mechanical, electrical engineering, integrated photonics et cetera.

Self-Organzation and Collaboration for Level 5 AGI¹⁰

I am also fascinated by this general principle of collaboration and self-organization as it is completely different from most of the currently hyped AI approaches with only a single agent operating in the world. But as I am writing this, we are slowly transitioning to the next level of AI where multiple LLMs are collaborating with each other in small teams e.g. to write software.

What I believe we can learn from GNCAs is just how necessary it is for such AI to be trained to collaborate with other instances of itself. It is not enough to just throw them into the world and clash with other AIs. But rather, one might imagine that it is necessary for AIs to train each other to collaborate just like humans train AIs to collaborate with them through RLHF¹¹.

We could create a simple game environment where instances of the same LLM are forced to collaborate to solve puzzles, training itself from feedback with itself. It will be interesting to see where multi-agent reinforcement learning (MARL)¹² and self-play¹³ approaches will take the field.

Conclusion

Growing Neural Cellular Automata represent a fascinating intersection of biology-inspired computation and modern machine learning techniques and I highly recommend you read the original paper¹ which goes into more detail and provides visually stunning animations and interactive demonstrations of their GNCAs for various structures.

While not a particularly popular research area as of this moment, I do believe we can learn a few things about the importance of self-organization. It is in fact possible to accomplish highly complex tasks in collaboration with other agents while only having extremely limited local information.

Code

You can find all the code to train GNCAs on images and reproduce the experiments here: Code on GitHub.

Citation

If you found this explainer article useful, consider citing it as:

@misc{wach2025gnca,
  author       = {Quentin Wach},
  title        = {Growing Neural Cellular Automata},
  year         = {2025},
  howpublished = {\url{https://quentinwach.com/blog/2025/06/10/gnca.html}},
  note         = {An educational explanation and implementation of Growing Neural Cellular Automata},
}

Introduction

Neural Cellular Automata

Perception

Channels

Filters

Implementation

Update

Update Layers

Stochastic Update

Living Cells

Implementation

Learning to Grow & Regenerate

Initilialization

Growing

Pool-Based Persistence

Regeneration

Personal Thoughts

Issues with Scaling

Temporal Damage

Further Biological Extensions

Artificial Life & Evolution

Design Optimization Problems

Self-Organzation and Collaboration for Level 5 AGI10

Conclusion

Code

Citation

References

Self-Organzation and Collaboration for Level 5 AGI¹⁰